高校数学・正弦定理と余弦定理

最大角，最小角

【単元の目次】《数学Ⅰ・Ａ》
• 数と式　 • 根号計算　• 場合の数.順列.組合せ　• 確率　 • ２次関数　• ２次不等式　 • 集合・命題・条件・証明　• 正弦定理,余弦定理

【単元内の目次】 • 正弦定理（解説）　• 正弦定理（問題）　• 分数型の方程式　• 余弦定理　• 三辺から角を求める問題　• 余弦定理を２次方程式として解く　• 三角形を解く　　　• 筆算だけで解く問題(1) 　• 筆算だけで解く問題(2) 　• 最大角・最小角　• 三角形の形状問題　• 三角形の証明問題　• ヘロンの公式　• 内接円の半径　• 正弦定理,余弦定理（共通,センター問題）

♪♥ この教材は，高校数学の基本問題のうち，最大角・最小角のマイナーチェンジありのカバー版です．
♫♣ 元の教材が通信トラブルなどで読めないときに，こちらを使ってください．なお，学習の記録は付いていません．

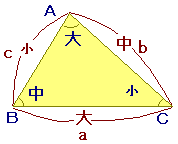
== 最大角，最小角 ==

《解説》
■　次の図のように，△ABCにおいて，

　a≦b≦cならばA≦B≦Cです.
（逆も成り立ちます.）

つまり，
「対辺が長い」ならば「角度が大きい」
（「角度が大きい」ならば「対辺が長い」）
といえます.・・・(1)

(証明) 余弦定理による証明･･･論理は簡単，変形はやや複雑
(方針) a≦b←→cos A≧cos B←→A≦Bを示す.
$\cos A-\cos B=\frac{b^2+ c^2-a^2}{2bc}-\frac{c^2+ a^2-b^2}{2ca}$
$=\frac{1}{2abc}\{a(b^2+ c^2-a^2)-b(c^2+ a^2-b^2)\}$

※分子は，a, bについて3次，cについて2次
→cについて整理する

$=\frac{1}{2abc}\{(a-b)c^2+ a(b^2-a^2)-b(a^2-b^2)\}$
$=\frac{1}{2abc}\{(a-b)c^2-(a^2-b^2)(a+ b)\}$
$=\frac{1}{2abc}\{(a-b)c^2-(a-b)(a+ b)^2\}$
$=\frac{1}{2abc}(a-b)\{c^2-(a+ b)^2\}$
$=\frac{1}{2abc}(a-b)(c-a-b)(c+ a+ b)$

ここで，a, b, c>0だからc+a+b>0
また，三角形の成立条件によりc<a+bだからc−a−b<0
ゆえに，
a≦b←→cos A≧cos B←→A≦Bが成り立つ．

(証明) 正弦定理による証明･･･論理は複雑，変形は少ない　「A≦B⇔a≦b」は，次の図を用いて示せる．

ア）A1≦B1≦90°のとき，正弦定理により
　a=2Rsin A1
　b=2Rsin B1 だからa≦b
イ） A2<90°<B2のとき，右図の○のときに，A2+B2=180°になって三角形ができないから，A2は○よりも小さな角度でなければならない．このとき，
sin A2≦sin B2となるから，ア）の場合と同様に正弦定理を用いて，a≦bが示せる．
　同様にして「B≦C⇔b≦c」も示せる．

■　△ABCにおいてA, B, Cのうち最も大ききな角度を最大角，最も小さな角を最小角と呼ぶと，右の図においては最大角はAで最小角はCです.
　(1)の関係から，最大角，最小角とその対辺の長さについて次のように言えます.

三角形において，
　　最大角には最大辺が対応する.
　　最小角には最小辺が対応する.

≪例≫
　三角形の３辺の長さが7, 8, 13のとき，この三角形の最大角を求めなさい.

（答案）
辺の長さ13が最も長いから，13に対応する角を求める.
$\cos\theta=\frac{7^2+ 8^2-13^2}{2\times 7\times 8}=\frac{-56}{112}=-\frac{1}{2}$
$\theta=120^{\circ}$ ･･･(答)

《問題1》
　三角形の３辺の長さが，次のように与えられているとき，この三角形の最大角を求めなさい.

　右の選択肢の中から正しいと思うものをクリックしてください．選択肢をクリックすれば，採点結果と解説が出ます．見ているだけでは解説は出ません．

(1)
　　17, 15, 8

解答を見る

17が最大辺だから，これに対応する角を求める
$\cos\theta=\frac{15^2+ 8^2-17^2}{2\times 15\times 8}=0$
⇒θ=90°･･･（答） →解答を隠す←

30°，45°，60°，90°

120°，135°，150°，上記以外

(2)
　　5, 16, 19

解答を見る

19が最大辺だから，これに対応する角を求める
$\cos\theta=\frac{5^2+ 16^2-19^2}{2\times 5\times 16}=-\frac{1}{2}$
⇒θ=120°･･･（答） →解答を隠す←

30°，45°，60°，90°

120°，135°，150°，上記以外

(3)
　　35, 43, 13

解答を見る

43が最大辺だから，これに対応する角を求める
$\cos\theta=\frac{35^2+ 13^2-43^2}{2\times 35\times 13}=-\frac{455}{910}=-\frac{1}{2}$
⇒θ=120°･･･（答） →解答を隠す←

30°，45°，60°，90°

120°，135°，150°，上記以外

(4)
　　 $1,\hspace{5}\sqrt{2},\hspace{5}\sqrt{5}$

解答を見る

$\sqrt{5}$ が最大辺だから，これに対応する角を求める
$\cos\theta=\frac{1+ 2-5}{2\times 1\times\sqrt{2}}=-\frac{2}{2\sqrt{2}}=-\frac{1}{\sqrt{2}}$
⇒θ=135°･･･（答） →解答を隠す←

30°，45°，60°，90°

120°，135°，150°，上記以外

《問題2》
　三角形の３辺の長さが，次のように与えられているとき，この三角形の最小角を求めなさい.

(1)
　　 $3\sqrt{3},\hspace{5}\sqrt{7},\hspace{5}4$

解答を見る

$3\sqrt{3}=\sqrt{27},\hspace{5}\sqrt{7},\hspace{5}4=~\sqrt{16}$ のうちで $\sqrt{7}$ が最小辺だから，これに対応する角を求める
$\cos\theta=\frac{27+ 16-7}{2\times3\sqrt{3}\times 4}=\frac{36}{24\sqrt{3}}=\frac{\sqrt{3}}{2}$
⇒θ=30°･･･（答） →解答を隠す←

30°，45°，60°，90°

120°，135°，150°，上記以外

(2)
　　 $3+\sqrt{3},\hspace{5}2\sqrt{3},\hspace{5}3\sqrt{2}$

解答を見る

$3+\sqrt{3}$ ≒4.7, $2\sqrt{3}$ ≒3.4, $3\sqrt{2}$ ≒4.2の中で， $2\sqrt{3}$ が最小辺だからこれに対応する角を求める
$\cos\theta=\frac{(3+\sqrt{3})^2+ 18-12}{2\times(3+\sqrt{3})\times 3\sqrt{2}}=\frac{6\sqrt{3}(1+\sqrt{3})}{6\sqrt{6}(1+\sqrt{3})}=\frac{1}{\sqrt{2}}$
⇒ θ=45° →解答を隠す←

30°，45°，60°，90°

120°，135°，150°，上記以外

《解説》
筆算で角度まで求められるのは，30°または45°の整数倍の角度に限られますが，cos θの値まででよいときはそのような制限はなくなります.

≪例≫
　三角形の3辺の長さが，次のように与えられているとき，この三角形について最大角の余弦を求めなさい.
　　a=9, b=8, c=7

(答案)
　aが最大なので，角Aが最大
　 $\cos A=\frac{64+ 49-81}{2\times 8\times 7}=\frac{32}{112}=\frac{2}{7}$ ･･･（答）

《問題3》　以下の問題は，採点方式にしていませんので，各自で解いて答え合わせを行ってください．
1

△ABCにおいて，sin A:sin B:sib C=5:6:7とする.最大角をθとするとき，cosθ=［　　］である.

（日本工大入試問題からの引用）

解答を見る

正弦定理によりsin A:sin B:sin C=a:b:c=5:6:7
⇒ a:b:c=5k:6k:7kとおけてcが最大だからCが最大角θになる
$\cos C=\frac{25+ 36-49}{2\times 5\times 6}=\frac{12}{60}=\frac{1}{5}$ →解答を隠す←

2
三角形の3つの高さを各々4, 9, 6とするとき，最小角の余弦を求めよ.

解答を見る

三辺の長さをa, b, cとおき，各々に対する高さをh1, h2, h3とおいて，面積Sを3通りに表すと辺の長さの比が分かる。
$S=\frac{ah_1}{2}=\frac{bh_2}{2}=\frac{ch_3}{2}$
$=\frac{4a}{2}=\frac{9b}{2}=\frac{6c}{2}$
だから
$a=\frac{S}{2},\hspace{5}b=\frac{2S}{9},\hspace{5}c=\frac{S}{3}$
したがって
a:b:c=9:4:6
bが最小だからBが最小角になる
a=9k, b=4k, c=6k (k>0)とおけるから
$\cos B=\frac{c^2+ a^2-b^2}{2ca}=\frac{36k^2+ 81k^2-16k^2}{2\times 6k\times 9k}$
$=\frac{101k^2}{108k^2}=\frac{101}{108}$ ･･･（答） →解答を隠す←

3
　△ABCの3辺がBC=x2−x+1, CA=x2−2x, AB=2x−1で表されている.
(1)　3つの辺の大小関係を調べよ.
(2)　△ABCの最大の内角はいくらか.

（静岡大入試問題からの一部引用）

解答を見る

(1)

（参考）
三角形の成立条件は，a,b,c>0･･･(1)(2)(3)
a+b>c, b+c>a, c+a>b･･･(4)(5)(6)
であるが，(4)(5)(6)が成り立てば(1)(2)(3)も成り立つから，「三角形の成立条件は(4)(5)(6)」としてよい

三角形の成立条件より
　(x2−x+1)+(x2−2x)>(2x−1)･･･(*1)
　(x2−2x)+(2x−1)>(x2−x+1)･･･(*2)
　(2x−1)+(x2−x+1)>(x2−2x)･･･(*3)
(*1)からx2−5x+2>0⇔ $x\lt\frac{1}{2},\hspace{3}x\gt 2$
(*2)からx>2
(*3)からx>0

以上の共通部分から，x>2

次に，x>2の範囲で，x2−x+1, x2−2x, 2x−1の大小関係を調べる

(x2−x+1)−(x2−2x)=x+1 (>0)だから

(x2−x+1)>(x2−2x)

(x2−x+1)−(2x−1)=x2−3x+2=(x−1)(x−2) (>0)だから

(x2−x+1)>(2x−1)

ここまでから，x2−x+1が最大であることが分かる．残り２つの大小関係を調べる．

(x2−2x)−(2x−1)<0となるxの値の範囲を求めると
x2−4x+1<0⇔ $2-\sqrt{3}\lt x\lt 2+\sqrt{3}$
x>2の範囲で検討しているから， $2\lt x\lt 2+\sqrt{3}$
よって，
ア） $2\lt x\lt 2+\sqrt{3}$ のとき

(x2−2x)<(2x−1)<(x2−x+1)

イ） $x\underset{=}{\gt}2+\sqrt{3}$ のとき

(2x−1)≦(x2−2x)<(x2−x+1)

(2)
BC=x2−x+1が最大であるから，角Aが最大
$\cos A=\frac{(x^2-2x)^2+(2x-1)^2-(x^2-x+ 1)^2}{2(x^2-2x)(2x-1)}$
この式の分子を展開してから，因数分解すると
$\cos A=\frac{-x(2x-1)(x-2)}{2(x^2-2x)(2x-1)}=-\frac{1}{2}$
よって， A=120°･･･（答） →解答を隠す←

4
　3辺の長さがx2+2x+4, x2−4, 4x+4である三角形の最大角を求めよ.

（桃山学院大学入試問題からの一部引用）

解答を見る

a=x2+2x+4 , b=x2−4 , c=4x+4とおく
はじめに三角形の成立条件からxの取りうる値の範囲を求める
a+b>c , b+c>a , c+a>bから

(x2+2x+4)+(x2−4)>(4x+4)を解くと

x<−1, 2<x

(x2−4)+(4x+4)>(x2+2x+4)を解くと

x>2

(4x+4)+(x2+2x+4)>(x2−4)を解くと

x>−2

これらの共通部分から，x>2…(1)

このとき
　　a−b=x2+2x+4−(x2−4)=2x+8>0
　　a−c=x2+2x+4−(4x+4)=x2−2x=x(x−2)>0
だからa>b, a>c ⇒ a=x2+2x+4が最大辺になる…(2)
$\cos A=\frac{(x^2-4)^2+(4x+ 4)^2-(x^2+ 2x+ 4)^2}{2(x^2-4)(4x+ 4)}$
分母分子を展開してから因数分解する
$\cos A=\frac{-4(x^2-4)(x+ 1)}{2(x^2-4)(4x+ 4)}=-\frac{1}{2}$
　⇒　A=120°･･･（答） →解答を隠す←

== 最大角，最小角 ==

コメント